It's only ambiguous if you're completely unfamiliar with the convention.
Agreed, the problem for some of us is that the convention changed within the last 30 years.I graduated high school in '82 so learned my mat in the late 70s and early 80s.
I was taught that -5^2 = negative five squared = -5*-5 = 25
It is now taught that -5^2 = negative
of five squared = -(5*5) = 25
I've seen the text books now and understand how the answer of -25 is achieved. It just seems unnatural to me and I will always see it as 25.
Huh?




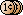
 There is a reason we have parentheses in math.
There is a reason we have parentheses in math.
 The math never changes. Sometimes as you get older you just don't remember things as well as you think you do.
The math never changes. Sometimes as you get older you just don't remember things as well as you think you do. It's a convention. Neither way is necessarily more or less "right" than the other, we pick one we all agree on and go with it. With that said, it's been agreed that -52 is -25, unless you specify otherwise with parentheses. I think that's probably a good way to handle it, given the way we usually think about and teach concepts like negative numbers and the commutativity of addition, etc. We typically treat the - sign as an operator on the natural number 5, and not as an inseperable part of the integer -5.
It's a convention. Neither way is necessarily more or less "right" than the other, we pick one we all agree on and go with it. With that said, it's been agreed that -52 is -25, unless you specify otherwise with parentheses. I think that's probably a good way to handle it, given the way we usually think about and teach concepts like negative numbers and the commutativity of addition, etc. We typically treat the - sign as an operator on the natural number 5, and not as an inseperable part of the integer -5. The math never changes. Sometimes as you get older you just don't remember things as well as you think you do.
The math never changes. Sometimes as you get older you just don't remember things as well as you think you do.